占星筆記No.1 機率是越乘越低的

持續提供免費塔羅占卜，詳情請見http://www.tarotlab.tw/

考慮一個問題：有兩個箱子，其中一個裡面有{A,B}而另一個裡裝的是{1,2,3}，那各抽一組會有幾種可能呢？答案其實就是全部列出來…如下圖

全部的可能有A1,A2,A3還有B1,B2,B3共6種可能。

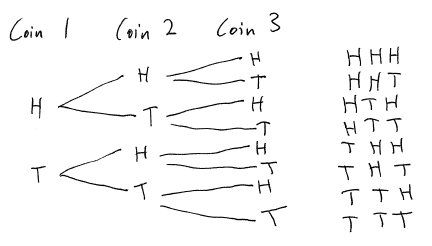
再換一個問題，如果丟有三個箱子，分別裝{H1,T1},{H2,T2},{H3,T3}，各抽一個的話全部會有幾種可能呢？如果把圖畫出來的話就可以發現有8種…

 

當然不可能每次遇到問題都畫樹狀圖出來嘛，我們可以發現兩個箱子的例子其實就是兩種情況(A或B選一個)交替配合三種情況(1,2,3)，因此是2×3=6種可能。而第二個例子自然就是2x2x2=8種可能囉。

從上面兩個例子我們可以發現，當箱子越多的時候全部的可能，可以發現一件事情，就是如果箱子越多的話因為所有的組合就越乘越多種…而且上升的速度是用乘的所以超快的。1變2、2變4、4變8…只要乘個10次就到1024種囉。

由於所有的組合會越來越多，換句話說特定一種組合的情況機率就越來越低了。於是這裡有一個違反大家直覺的生日問題…當一個房子裡有10個人的話有兩個人生日完全一樣機率有多少呢？直覺的想，一年全部有365天只有10個人那機率應該很低吧…不過開始計算的話可以發現

第一個人隨便選一天都一定不重複，所以不重複的機率是365/365=1
第二個人少了一天可以選，所以不重複的機率剩364/365
第三個人少了兩天可以選，所以不重複的機率剩363/365
…
第10個人少了9天可以選，所以不重複的機率剩356/365

全部乘起來變成不重複的機率是(365/365)x(364/365)x(363/365)x…x(356/365)=88.3%。換句話說10個人如果有大約12%的機會會有人生日相同哦。大概每十次就會遇到一次這種情況和我們的直覺很不一樣吧。順道一提，由下表可以發現大概23個人就可以有一半的機會遇到生日相同的人…因此下次遇到在團體或是聚會裡遇到有人生日一樣的話就不用太呀異了。

人數	有兩人生日相同的機率
5	2.7%
10	11.7%
20	41.1%
23	50.7%
30	70.6%
40	89.1%

 

參考資料

Wikipedia: Rule of product
http://en.wikipedia.org/wiki/Rule_of_product

York大學的講義
http://faculty.ycp.edu/~dhovemey/fall2006/mat111/lecture/lecture36.html

Wikipedia: 生日問題
http://zh.wikipedia.org/wiki/%E7%94%9F%E6%97%A5%E5%95%8F%E9%A1%8C