占星筆記No.3 總是有鴿子要擠一起的
持續提供免費塔羅占卜,詳情請見http://www.tarotlab.tw/
最近遇到一個有趣的”巧合”,讓人想到鴿籠原理,但因為鴿籠原理裡的鴿子要擠在一起住很可憐所以這篇文章標題變成”總是有鴿子要擠一起的”
首先先來講一下鴿籠原理,如果有n+1隻鴿子要住在n個籠子裡,那其中至少有一個籠子裡有兩隻(含)以上的鴿子。
簡單的考慮n=9的情況好了,那上面那句話變成10隻鴿子要住在9個籠子裡,那其中至少有一個籠子裡有兩隻(含)以上的鴿子。證明的方式如下圖,
 我們可以發現第10隻鴿子不論住到哪裡都會使得某個籠子裡有兩隻鴿子。
我們可以發現第10隻鴿子不論住到哪裡都會使得某個籠子裡有兩隻鴿子。
鴿籠原理在生活上的應用大概就是停電的時候了吧…如果您要在停電的黑夜裡從衣櫃之中拿出要穿的襪子,當然有一個辦法就是把襪子全部拿出來然後一件一件對。不過仔細思考一下,由於平常只買黑色、白色、藍色的襪子(3個鴿籠),那只要拿出四支襪子(4支鴿子)因為鴿籠原理的關係會使得兩支襪子是同一種顏色的(2隻鴿子住在同一個籠子裡)。這樣子就不會那麼辛苦了…
接著說說最近在宴會遇到的巧合,在一次的巧遇裡一共有六個人,然後我們發現剛好有三個人彼此兩兩互相認識,其實這個”巧合”也是鴿籠原理哦…
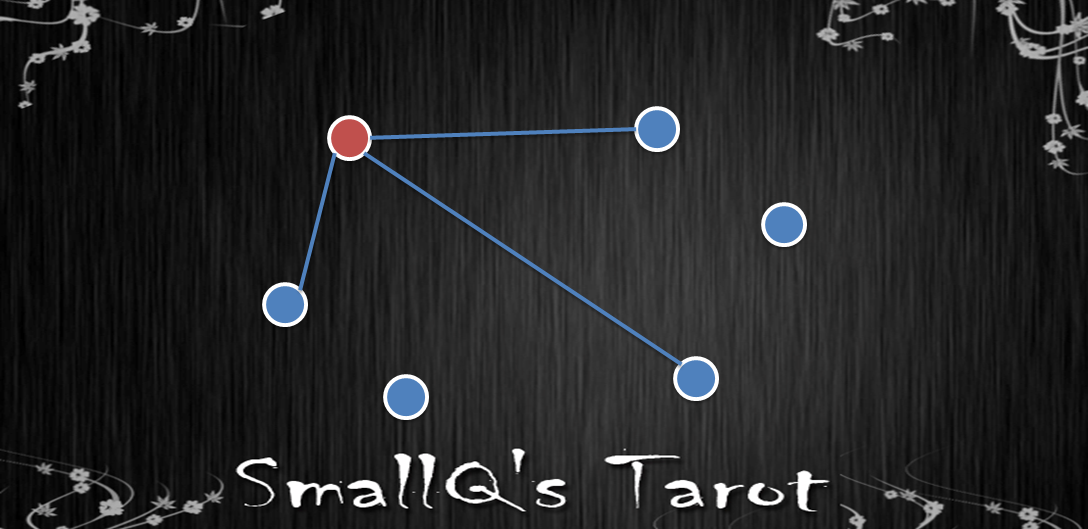
六個人就像下圖中六個點,隨便抓一個A出來好了,那剩下五個人裡可以分成兩群:認識A的和不認識A的。五隻鴿子住到兩個籠子裡的話那其中至少有某個籠子要擠三隻鴿子哦(這次比較可憐)。換句話說這五個人裡至少會有三個人要嘛都認識A要嘛都不認識A,SmallQ先畫出藍色的實線代表這個關係。
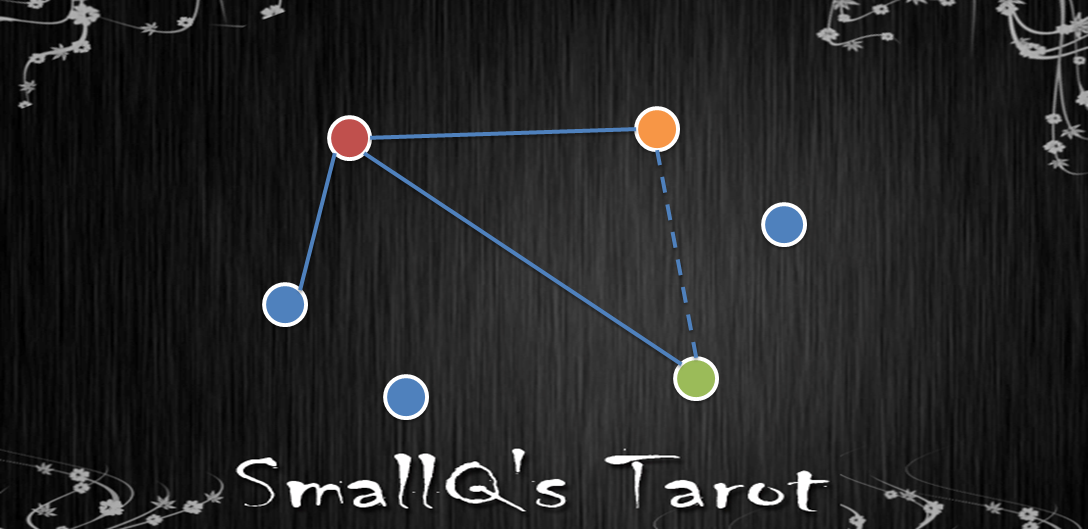
接著從這三個人裡隨便找出一個人(如下圖的橘點),他和其他人的關係就不能是實線了,否則像紅、橘、綠三點就圍出一個實線的三角形,那紅、橘、綠三個人就兩兩認識(或不認識)了。
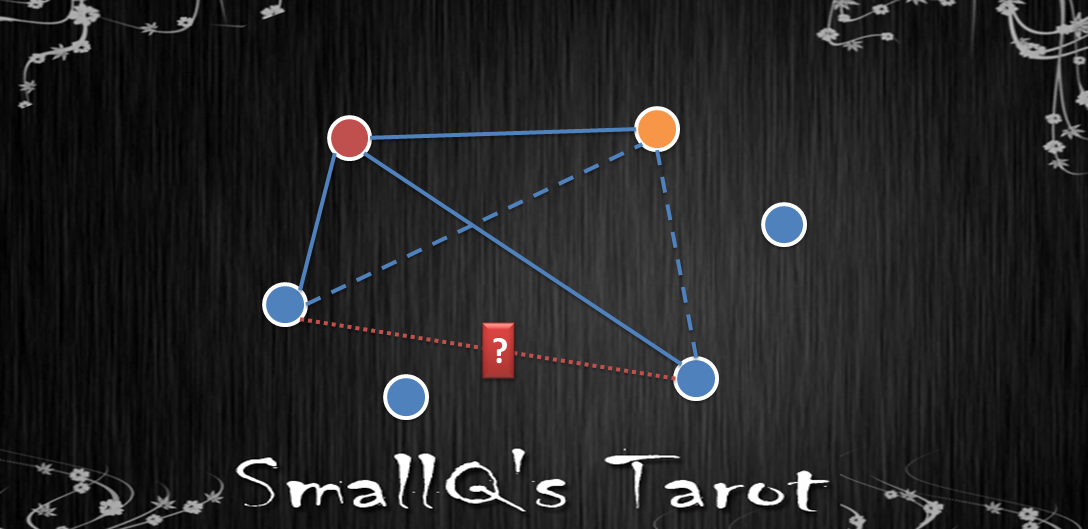
最後就變成下圖,有一條問號的線需要討論,但不論是實線或是虛線都會使得至少有三個人彼此兩兩認識,或是兩兩不認識。
由於這是必然的”巧合”,或許可以當您下次在某宴會或是活動的開場白呢!(當然證明就不用說了…XD)
參考資料
維基百科:鴿巢原理
http://zh.wikipedia.org/wiki/%E9%B4%BF%E5%B7%A2%E5%8E%9F%E7%90%86
數學傳播期刊
http://episte.math.ntu.edu.tw/articles/mm/mm_02_4_07/page2.html